期权定价公式旨在确定公平合理的期权价格，使得买卖双方在交易中达到利益相对平衡。一个完善的期权定价模型能够帮助投资者理解影响期权价格的关键因素，并据此进行风险管理和策略制定。期权定价公式的推导是一个复杂的过程，涉及到概率论、随机过程、和微分方程等多个数学工具。将重点介绍布莱克-斯科尔斯模型（Black-Scholes Model）的推导过程，因为该模型是期权定价领域中最具影响力和广泛应用的模型之一。虽然有很多更复杂的模型，但Black-Scholes模型提供了理解期权定价逻辑的坚实基础。

风险中性定价原理

风险中性定价是期权定价的核心思想之一。它假设投资者对风险是中性的，这意味着投资者只关心预期收益，而不关心收益的波动性（风险）。在这种假设下，所有资产的预期收益率都等于无风险利率。虽然现实世界并非如此，但风险中性定价提供了一种在数学上简化期权定价问题的有效方法。通过将世界假设为风险中性的，我们可以使用无风险利率对期权未来的预期支付进行贴现，而无需考虑投资者的风险偏好。

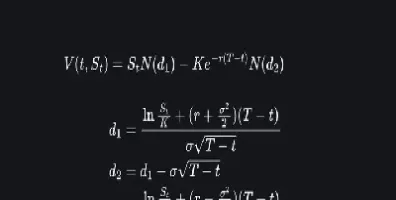
具体来说，风险中性定价背后的逻辑是：如果期权和标的资产之间存在套利机会（即，通过同时买卖期权和标的资产，在无风险的情况下获得利润），那么市场力量会迅速消除这种套利机会，从而将期权价格调整到与其内在价值一致的水平。在没有套利机会的情况下，期权的价格必须等于其风险中性预期收益的现值。

构建复制组合

复制组合（Replicating Portfolio）是期权定价的关键概念。它的基本思想是：我们可以通过买卖标的资产和无风险债券来构建一个组合，该组合的收益与期权的收益完全相同。换句话说，我们可以通过组合标的资产和无风险债券来完全复制期权的风险和回报。如果我们可以成功地构建出一个复制组合，那么期权的价格就应该等于该复制组合的成本。

在Black-Scholes模型中，我们假设可以随时调整复制组合中的标的资产和无风险债券的比例，以便始终保持与期权相同的收益。这种动态调整是Black-Scholes模型的关键假设之一。动态复制的策略意味着我们需要根据标的资产价格的变化不断调整组合中的头寸，以确保组合的收益与期权的收益始终匹配。这个调整过程涉及到计算称为“Delta”的希腊值，它表示期权价格对标的资产价格变化的敏感度。

随机微分方程和伊藤引理

Black-Scholes模型假设标的资产的价格遵循几何布朗运动（Geometric Brownian Motion）。这是一种描述资产价格随机变化的数学模型，它假设资产价格的变化是随机的，并且遵循一定的概率分布。几何布朗运动可以用一个随机微分方程来表示：

dSt = μSt dt + σSt dWt

其中，St 是标的资产在时间 t 的价格，μ 是资产的预期收益率，σ 是资产价格的波动率，dWt 是标准的维纳过程（Wiener Process），它表示一个随机的增量。这个方程说明，资产价格的变化由两部分组成：一部分是与预期收益率成比例的漂移项（μSt dt），另一部分是与波动率和随机增量成比例的扩散项（σSt dWt）。

伊藤引理（Itô's Lemma）是期权定价中另一个重要的数学工具。它用于计算一个函数（该函数是标的资产价格和时间的函数）的随机微分。在Black-Scholes模型中，我们需要知道期权价格（C）随标的资产价格（S）和时间（t）变化的规律。伊藤引理可以帮助我们做到这一点。简单来说，伊藤引理告诉我们如何对一个随机变量的函数求导，从而得到该函数随时间变化的表达式。

假设期权价格 C 是标的资产价格 S 和时间 t 的函数，即 C = f(S, t)，那么根据伊藤引理：

dC = (∂C/∂t + μS(∂C/∂S) + 1/2 σ²S²(∂²C/∂S²)) dt + σS(∂C/∂S) dWt

这个公式描述了期权价格变化的随机过程，它与标的资产价格变化的随机过程密切相关。

推导Black-Scholes偏微分方程

现在，我们可以结合风险中性定价、复制组合和伊藤引理来推导出Black-Scholes偏微分方程。设 π 表示复制组合的价值，π = -ΔS + C，其中 Δ 是我们在标的资产上的持有头寸，C 是期权的价格。我们可以选择 Δ 使得复制组合的收益与期权的收益完全相同。这意味着我们要在标的资产价格上涨时卖出，价格下跌时买入。通过精巧的代数运算和伊藤引理，我们可以证明：

dπ = -Δ dS + dC

为了确保复制组合的收益与期权的收益完全相同，我们需要选择 Δ 使得随机项消除。也就是说，我们需要：

Δ = ∂C/∂S

这意味着 Δ 应该是期权价格对标的资产价格的一阶导数，也称为期权的 Delta。在这种情况下，复制组合就变成了无风险的投资，因此它的收益必须等于无风险利率乘以组合的价值：

dπ = rπdt = r(-ΔS + C)dt

将 dπ 和 dC 的表达式代入并化简，我们可以得到Black-Scholes偏微分方程：

∂C/∂t + 1/2 σ²S²(∂²C/∂S²) + rS(∂C/∂S) - rC = 0

这个偏微分方程描述了期权价格随时间变化的规律，其中 σ 是标的资产价格的波动率，r 是无风险利率。要解决这个偏微分方程，我们需要指定边界条件，即期权在到期时的支付函数。对于欧式看涨期权，到期时的支付函数是：C(S,T) = max(S - K, 0)，其中 K 是执行价格，T 是到期时间。

求解 Black-Scholes 方程得到期权定价公式

通过使用各种数学技巧（例如，变量替换和求解扩散方程），可以解决上述偏微分方程并得到 Black-Scholes 期权定价公式。 对于欧式看涨期权，公式如下：

C = S N(d1) - K e^(-rT) N(d2)

其中：

d1 = [ln(S/K) + (r + σ²/2) T] / (σ √T)

d2 = d1 - σ √T

S 是标的资产的当前价格，K 是执行价格，r 是无风险利率，T 是到期时间（以年为单位），σ 是标的资产价格的波动率，N(x) 是标准正态分布的累积分布函数。

这个公式表明，欧式看涨期权的价格取决于标的资产价格、执行价格、无风险利率、到期时间和波动率。波动率是影响期权价格的重要因素，因为它反映了市场对标的资产价格未来波动程度的预期。

总而言之，Black-Scholes期权定价公式的推导过程涉及风险中性定价、复制组合、随机微分方程、伊藤引理和求解偏微分方程等重要的数学概念。虽然Black-Scholes模型存在一些局限性（例如，假设波动率是恒定的），但它仍然是期权定价领域中最具影响力和实用性的模型之一。